draw parabola in civil 3d
Ray is a licensed engineer in the Philippines. He loves to write well-nigh mathematics and ceremonious engineering science.
What Is a Parabola?
A parabola is an open plane curve that is created by the junction of a correct round cone with a plane parallel to its side. The set of points in a parabola are equidistant from a fixed line. A parabola is a graphical illustration of a quadratic equation or second-degree equation. Some of the examples representing a parabola are the projectile motion of a body that follows a parabolic curve path, suspension bridges in the shape of a parabola, reflecting telescopes, and antennae. The general forms of a parabola are:
Cyii + Dx +Ey + F = 0
where C ≠ 0 and D ≠ 0
Ax2 + Dx + Ey + F = 0
where A ≠ 0 and D ≠ 0
Different Forms of Parabolic Equations
The full general formula Cy2 + Dx +Ey + F = 0 is a parabolic equation whose vertex is at (h, g) and the bend opens either to the left or right. The two reduced and specific forms of this general formula are:
(y - k)ii = 4a (x - h)
(y - k)2 = - 4a (x - h)
On the other hand, the general formula Ax2 + Dx + Ey + F = 0 is a parabolic equation whose vertex is at (h, k) and the curve opens either upward or downwardly. The two reduced and specific forms of this full general formula are:
(x - h)2 = 4a (y - 1000)
(10 - h)ii = - 4a (y - k)
If the vertex of the parabola is at (0, 0), these general equations accept reduced standard forms.
y2 = 4ax
y2 = - 4ax
102 = 4ay
Read More From Owlcation
10two = - 4ay
Properties of a Parabola
A parabola has half-dozen properties.
one. The vertex of a parabola is at the center of the curve. Information technology can either be at the origin (0, 0) or any other location (h, k) in the Cartesian aeroplane.
2. The concavity of a parabola is the orientation of the parabolic curve. The curve may open either upward or downward, or to the left or right.
three. The focus lies on the axis of symmetry of a parabolic bend. It is a altitude 'a' units from the vertex of the parabola.
4. The centrality of symmetry is the imaginary line containing the vertex, focus, and the midpoint of the directrix. It is the imaginary line that separates the parabola into ii equal sections mirroring each other.
| Equation in Standard Class | Vertex | Concavity | Focus | Axis of Symmetry |
|---|---|---|---|---|
| y^2 = 4ax | (0, 0) | right | (a , 0) | y = 0 |
| y^2 = -4ax | (0, 0) | left | (-a, 0) | y = 0 |
| (y - k)^2 = 4a (x - h) | (h, chiliad) | correct | (h + a, thou) | y = chiliad |
| (y - k)^ii = -4a (10 - h) | (h, k) | left | (h - a, k) | y = chiliad |
| 10^two = 4ay | (0, 0) | upward | (0, a) | x = 0 |
| x^2 = -4ay | (0, 0) | downward | (0, -a) | x = 0 |
| (x - h)^ii = 4a (y - k) | (h, 1000) | upwards | (h, k + a) | x = h |
| (10 - h)^two = -4a (y - 1000) | (h, chiliad) | downwardly | (h, k - a) | x = h |
v. The directrix of a parabola is the line that is parallel to both axes. The altitude of the directrix from the vertex is 'a' units from the vertex and '2a' units from the focus.
6. Latus rectum is a segment passing through the parabolic curve'due south focus. The ii ends of this segment prevarication on the parabolic bend (±a, ±2a).
| Equation in Standard Form | Directrix | Ends of Latus Rectum |
|---|---|---|
| y^2 = 4ax | x = -a | (a, 2a) and (a, -2a) |
| y^ii = -4ax | ten = a | (-a, 2a) and (- a, -2a) |
| (y - grand)^two = 4a (x - h) | ten = h - a | (h + a, yard + 2a) and (h +a, thou - 2a) |
| (y - k)^2 = -4a (x - h) | x = h + a | (h - a, k + 2a) and (h - a, k - 2a) |
| x^2 = 4ay | y = -a | (-2a, a) and (2a, a) |
| ten^two = -4ay | y = a | (-2a, -a) and (2a, -a) |
| (10 - h)^2 = 4a (y - k) | y = yard - a | (h - 2a, thousand + a) and (h + 2a, k + a) |
| (ten - h)^2 = -4a (y - k) | y = yard + a | (h - 2a, k - a) and (h + 2a, k - a) |
Dissimilar Graphs of a Parabola
The focus of a parabola is due north units away from the vertex and is directly on the right side or left side if it opens to the right or left. On the other hand, the focus of a parabola is directly above or below the vertex if it opens upwards or downwardly. If the parabola opens to the right or left, the centrality of symmetry is either the x-axis or parallel to the x-axis. If the parabola opens upward or downward, the axis of symmetry is either the y-axis or parallel to y-axis. Here are the graphs of all equations of a parabola.
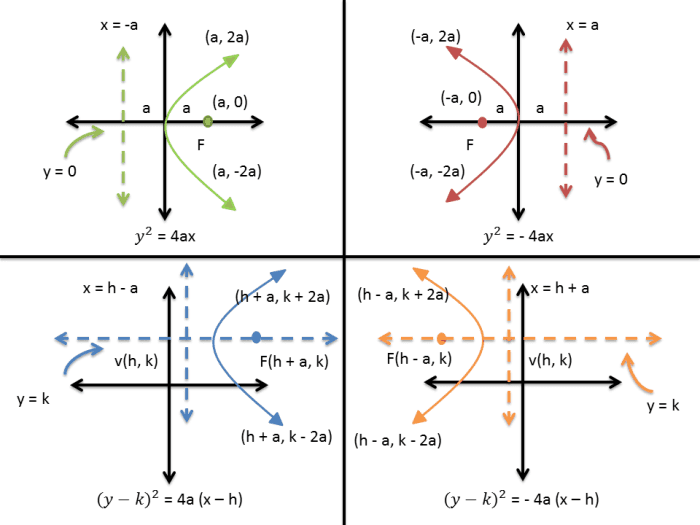
Graph of Different Equations of a Parabola
John Ray Cuevas
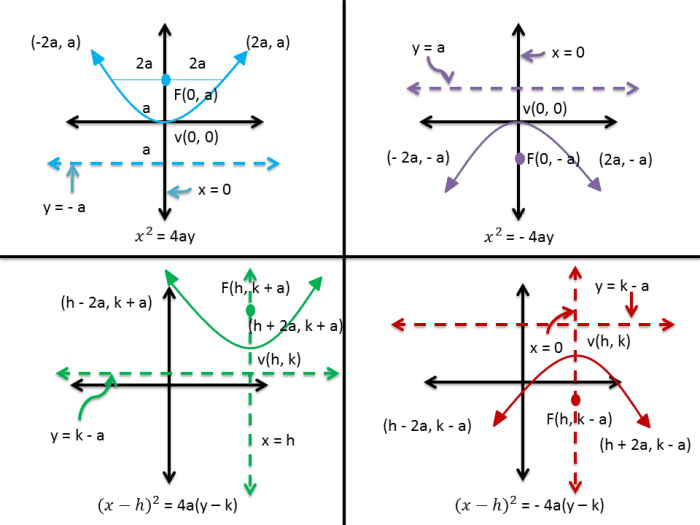
Graph of Different Forms of Parabola
John Ray Cuevas
Step-by-Step Guide on How to Graph a Parabola
1. Place the concavity of the parabolic equation. Refer for the directions of the opening of the bend to the given table in a higher place. It could be opening to the left or correct, or up or downward.
2. Locate the vertex of the parabola. The vertex can either exist (0, 0) or (h, k).
3. Locate the focus of the parabola.
4. Identify the coordinate of the latus rectum.
v. Locate the directrix of the parabolic bend. The location of the directrix is the aforementioned distance of the focus from the vertex but in the contrary direction.
vi. Graph the parabola by drawing a curve joining the vertex and the coordinates of the latus rectum. And so to stop information technology, label all the pregnant points of the parabola.
Problem i: A Parabola Opening to the Correct
Given the parabolic equation, y2 = 12x, determine the following properties and graph the parabola.
a. Concavity (management in which the graph opens)
b. Vertex
c. Focus
d. Latus rectum coordinates
eastward. The line of symmetry
f. Directrix
Solution
The equation y2 = 12x is in the reduced course y2 = 4ax where a = 3.
a. The concavity of the parabolic bend is opening to the right since the equation is in the form y2 = 4ax.
b. The vertex of the parabola with a grade y2 = 4ax is at (0, 0).
c. The focus of a parabola in the form ytwo = 4ax is at (a, 0). Since 4a is equal to 12, the value of a is 3. Therefore, the focus of the parabolic curve with equation ytwo = 12x is at (3, 0). Count iii units to the right.
d. The latus rectum coordinates of the equation yii = 4ax is at (a, 2a) and (a, -2a). Since the segment contains the focus and is parallel to the y-axis, we add together or subtract 2a from the y-centrality. Therefore, the latus rectum coordinates are (3, 6) and (3, -6).
e. Since the parabola'southward vertex is at (0, 0) and is opening to the correct, the line of symmetry is y = 0.
f. Since the value of a = 3 and the graph of the parabola opens to the right, the directrix is at x = -3.
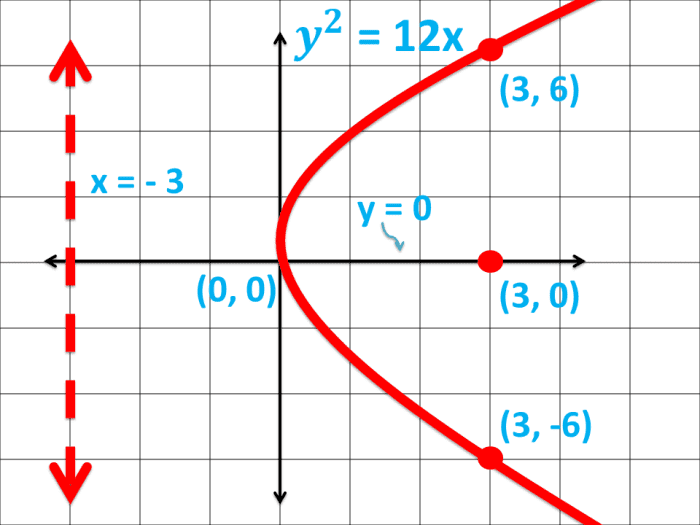
How to Graph a Parabola: Graph of a Parabola Opening to the Correct in Cartesian Coordinate System
John Ray Cuevas
Problem 2: A Parabola Opening to the Left
Given the parabolic equation, yii = - 8x, decide the following properties and graph the parabola.
a. Concavity (direction in which the graph opens)
b. Vertex
c. Focus
d. Latus rectum coordinates
east. The line of symmetry
f. Directrix
Solution
The equation y2 = - 8x is in the reduced form y2 = - 4ax where a = ii.
a. The concavity of the parabolic curve is opening to the left since the equation is in the form y2 = - 4ax.
b. The vertex of the parabola with a class y2 = - 4ax is at (0, 0).
c. The focus of a parabola in the form yii = - 4ax is at (-a, 0). Since 4a is equal to 8, the value of a is 2. Therefore, the focus of the parabolic bend with equation yii = - 8x is at (-2, 0). Count 2 units to the left.
d. The latus rectum coordinates of the equation y2 = - 4ax is at (-a, 2a) and (-a, -2a). Since the segment contains the focus and is parallel to the y-axis, we add together or subtract 2a from the y-axis. Therefore, the latus rectum coordinates are (-2, 4) and (-2, -4).
due east. Since the parabola's vertex is at (0, 0) and is opening to the left, the line of symmetry is y = 0.
f. Since the value of a = two and the graph of the parabola opens to the left, the directrix is at x = ii.
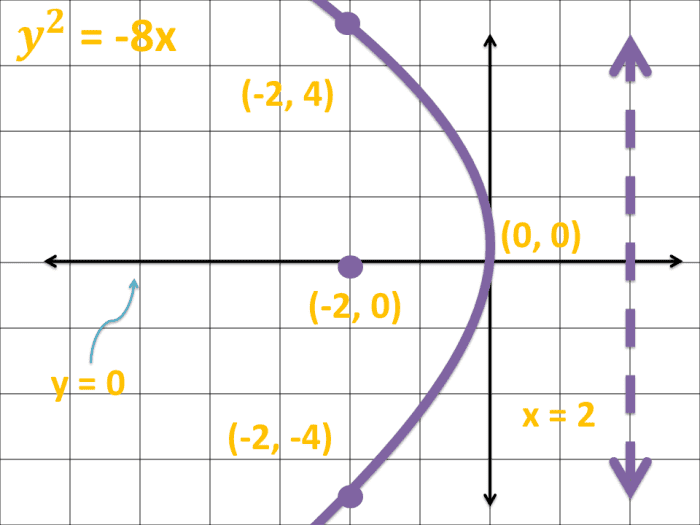
How to Graph a Parabola: Graph of a Parabola Opening to the Left in Cartesian Coordinate Organisation
John Ray Cuevas
Trouble 3: A Parabola Opening Upward
Given the parabolic equation tenii = 16y, determine the following properties and graph the parabola.
a. Concavity (direction in which the graph opens)
b. Vertex
c. Focus
d. Latus rectum coordinates
east. The line of symmetry
f. Directrix
Solution
The equation x2 = 16y is in the reduced form 102 = 4ay where a = 4.
a. The concavity of the parabolic curve is opening upward since the equation is in the class 102 = 4ay.
b. The vertex of the parabola with a form tentwo = 4ay is at (0, 0).
c. The focus of a parabola in the form xii = 4ay is at (0, a). Since 4a is equal to 16, the value of a is iv. Therefore, the focus of the parabolic bend with equation x2 = 4ay is at (0, 4). Count four units upward.
d. The latus rectum coordinates of the equation xii = 4ay is at (-2a, a) and (2a, a). Since the segment contains the focus and is parallel to the x-centrality, nosotros add together or subtract a from the x-centrality. Therefore, the latus rectum coordinates are (-16, 4) and (16, four).
eastward. Since the parabola'southward vertex is at (0, 0) and is opening up, the line of symmetry is x = 0.
f. Since the value of a = four and the graph of the parabola opens upwardly, the directrix is at y = -four.
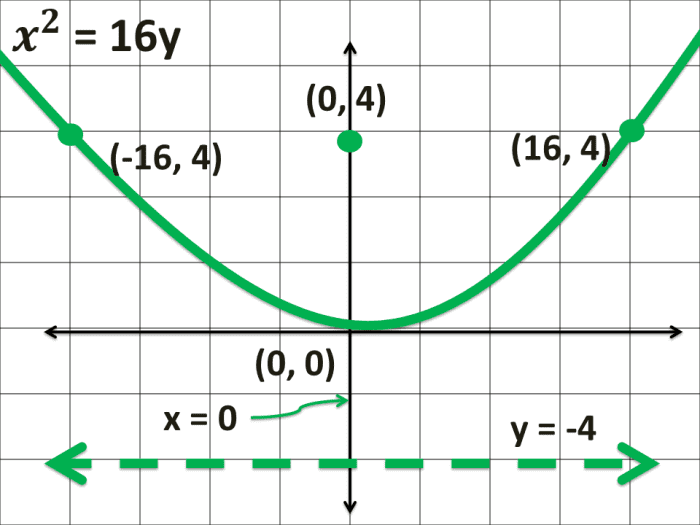
How to Graph a Parabola: Graph of a Parabola Opening Upward in Cartesian Coordinate System
John Ray Cuevas
Trouble iv: A Parabola Opening Downward
Given the parabolic equation (x - 3)ii = - 12(y + 2), determine the following properties and graph the parabola.
a. Concavity (direction in which the graph opens)
b. Vertex
c. Focus
d. Latus rectum coordinates
e. The line of symmetry
f. Directrix
Solution
The equation (x - 3)2 = - 12(y + 2) is in the reduced form (x - h)two = - 4a (y - k) where a = 3.
a. The concavity of the parabolic curve is opening downward since the equation is in the form (x - h)2 = - 4a (y - g).
b. The vertex of the parabola with a class (x - h)2 = - 4a (y - thousand) is at (h, k). Therefore, the vertex is at (3, -two).
c. The focus of a parabola in the class (10 - h)2 = - 4a (y - k) is at (h, grand-a). Since 4a is equal to 12, the value of a is iii. Therefore, the focus of the parabolic curve with equation (ten - h)2 = - 4a (y - k) is at (3, -5). Count 5 units downward.
d. The latus rectum coordinates of the equation (ten - h)2 = - 4a (y - k) is at (h - 2a, chiliad - a) and (h + 2a, k - a) Therefore, the latus rectum coordinates are (-iii, -five) and (9, v).
e. Since the parabola's vertex is at (3, -2) and is opening downwards, the line of symmetry is x = three.
f. Since the value of a = 3 and the graph of the parabola opens downwardly, the directrix is at y = one.
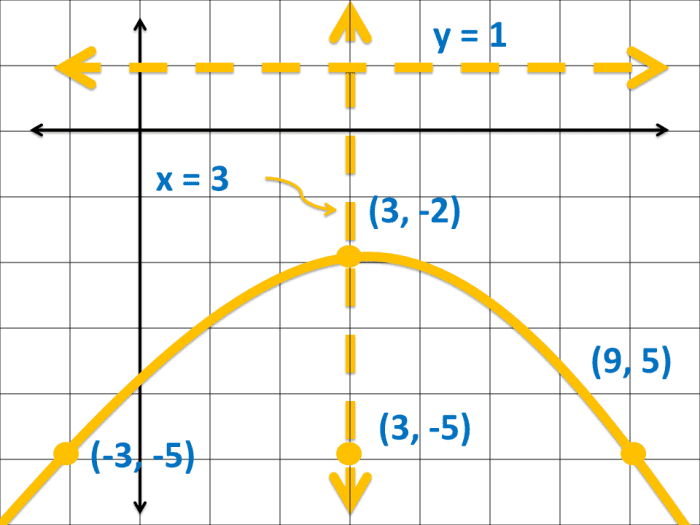
How to Graph a Parabola: Graph of a Parabola Opening Downwards in Cartesian Coordinate System
John Ray Cuevas
Learn How to Graph Other Conic Sections
- How to Graph an Ellipse Given an Equation
Learn how to graph an ellipse given the general form and standard form. Know the dissimilar elements, properties, and formulas necessary in solving problems about ellipse. - How to Graph a Circle Given a General or Standard Equation
Acquire how to graph a circle given the general form and standard form. Familiarize with converting full general form to standard form equation of a circle and know the formulas necessary in solving problems about circles.
This content is accurate and true to the all-time of the author's knowledge and is not meant to substitute for formal and individualized advice from a qualified professional.
Questions & Answers
Question: Which software tin can I employ to graph a parabola?
Answer: Yous can easily search for parabola generators online. Some popular online sites for that are Mathway, Symbolab, Mathwarehouse, Desmos, etc.
© 2022 Ray
Ray (author) from Philippines on June xxx, 2018:
I hope you and your boy are enjoying. Graphing parabolas are piece of cake given you are knowledgeable of the unlike properties and familiar with the equations.The tables provided would be a not bad help. Thank you over again, Sir Eric!
Eric Dierker from Spring Valley, CA. U.S.A. on June xxx, 2018:
Very interesting. I am just going to read it and not endeavour to pass a examination. Cheers
We are are working on the concepts of graphs.
Source: https://owlcation.com/stem/How-to-Graph-Different-Forms-of-Parabola
0 Response to "draw parabola in civil 3d"
Post a Comment